前回は代数学のまとめとして「数学の決闘」についてお話ししました。今回は新しい数学として、「解析学」についてお話ししていきます。

～解析学の誕生～

　幾何学から代数学が誕生し、数式が複雑化したころに一つの問題が発生する。

「この数式、複雑すぎて分からん」

この問題は数多の数学者からしたら大したことは無いのかもしれないが、一般庶民からしたら「数や文字だけで表されていて何を言っているのかわからない」となるのは自明の理である。この問題の解決の糸口になったのは、ルネ・デカルトが開発したデカルト座標系である。

～デカルトとデカルト座標系～

　1596年、フランスで生まれたルネ・デカルトは1600年代を代表する「哲学者」である。
元を辿れば哲学も数学も自然哲学ではあるが、この世の真理を追究する哲学者という数学者とは違う視点が、新しい発想を生み出す。

「数式が分からないなら、図にすればいいじゃない」(マリーアントワネット風)

　やはり、数式のみより図など可視化されたものの方が分かりやすいという発想である。これ自体は代数学を幾何学で表すだけに思えるが、デカルトの発想は違った。数学における関係式から点を打っていく。そう、グラフの誕生である。このｘ軸とｙ軸による直交座標をデカルト座標系と呼ぶのである。

～デカルト座標系の利点～

　読者の方の中には苦しめられた人もいるであろう、この「グラフ」という考えの利点をお話ししよう。例えば

　という式があるとしよう。ｘ＝0のときｙ＝5、ｘ＝2のときｙ＝1、・・・と特定の値についてはわかるが、「ｘの値によって、どのようにｙの値が変化していくのか」これをイメージするのは難しい、そこでデカルトはｘｙ座標平面を作り、この点をいくつも打ち繋げることで、この数式を可視化することに成功する、これが小学校から習うグラフである。

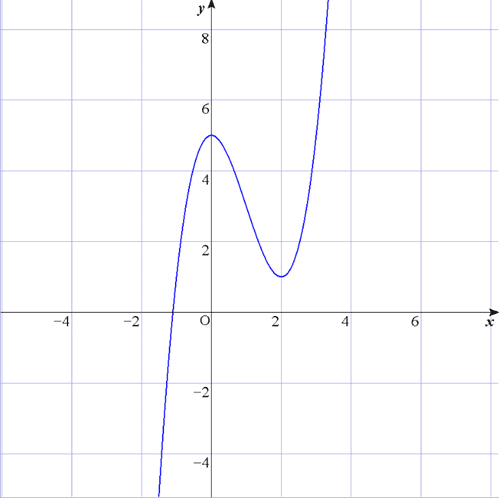
のグラフ

　このグラフにより、数式を図でイメージすることや、増減の傾向、最大値最小値など、必要な情報が汲み取れるようになる。この数式をグラフ化し、数式の性質を研究する分野を解析学と呼ぶ。

～微分・積分の誕生～

　グラフの話をすると合わせて話をしないといけないのが微分と積分である。高校数学を経験すると、「微分と積分はワンセット」と言うイメージがあるが、実はこの二つ全く関係のない生まれ方をしている。ここで微分と積分のおさらいをしておこう。

微分：平均変化率の収束を用いた関数変換法。用途として多いのが、一階微分の方程式を用いた、接線の傾きを求めることや二階微分の方程式を用いた変曲点の算出が挙げられる。つまり、関数や傾きの増減の傾向を見るために用いるのが微分である。また、式における次元を一つ下げる。

積分：面積を求める方法。これは長方形や三角形など、面積公式が古来からあるもの以外の曲線などにも用いることが可能。また、式における次元を一つ上げる。

このように、微分と積分は目的や用途が全く違うものとなっている。共通点としては二つある。一つは両方「次元操作の方法」であること、もう一つは両方「開発者が同じ人間」であること。この開発者と言うのが、アイザック・ニュートンとゴットフリート・ライプニッツである。

～解析学の大数学者ニュートンとライプニッツ～

　1600年代の数学者であるニュートンとライプニッツは、生まれた場所は違うが、生まれた時期が同じで、お互い違う方法で同じ研究をしたという珍しい組合せである。まずは聞きなじみのあるニュートンから話していこう。

　ニュートンは一般的には物理学者として有名だろう。理由としては「りんごが木から落ちた」話しが有名すぎる点にある。そう、万有引力の法則の発見だ。

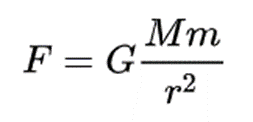
万有引力の法則とは、二つの物体に対して、お互いに引き寄せあう力が働いていることを言う。例えば「りんごが木から落ちた」とするならば、「りんご」と「地球」の二つの物体はお互いに引き寄せあう力が働いていることになる。このとき、質量の大きい方に引っ張られるので、りんごは地球に引き寄せられ木から落ちたということになる。

この力の計算を精密に行うためにニュートンが開発したのが積分である。また、この力の傾向を読み解くときに、微小区間において力がどのように働いているかを考える上で開発されたのが微分となっている。

　ちなみにこのニュートン、幼少期の家庭環境が複雑であったこともあり、情緒が不安定であったことでも有名である。当時の哲学者であるロバート・フックとの手紙で急に怒り出し、次の手紙で謝ったとの逸話が残っている。

　イギリスのニュートンに対して、ライプニッツはドイツの数学者である。数学者とは言ったが、その才能は多岐にわたり、哲学や科学はもちろん、博士号を得た法学を生かして外交官にもなった。

　ライプニッツの数学者としての特徴は、数学以外の分野にも精通していることから、「数学以外の分野を論理学として統一する」と言うことにある。そのベースになる代数学における集合や論理、演算の一環として微分・積分を発明することになる。また、その過程で２進法が開発されているである。

　晩年はプロイセン王に助言し、プロイセン科学アカデミーを設立。初代の会長に就任した。

　この二人によって考えられた微分と積分は、もともと別の目的で作られたものだが、この二つが逆操作であることを示す「微分積分学の基本定理」を発見したことから、現在の「微分と積分はワンセット」という発想に至る。

　今回は、代数をグラフ化して考える「解析学」についてお話ししました。表現力が問われる昨今ですが、数学においても「わかりやすい」「わかりづらい」があるので、グラフという目で見てわかる形を考えたのは、素晴らしい発明だと思います。
この後、微分・積分の表記法がライプニッツによるものが広まったこともあり、この後はドイツによる数学が飛躍的に発展していきます。

　次回はライプニッツによるドイツ数学の系譜をお話ししたいと思います！数学が好きな人も、数学に少しでも興味が沸いた人も、また見てくださいね！