初めましての方は初めまして！前回の記事を見てくれた方はお久しぶりです！正則学園の数学屋さんことHN.つるぎ先生です！

　前回は、「幾何学」という数学の誕生についてお話しました。今回は誕生した幾何学をさらなるものに発展させた二人の数学者を紹介します！

～数学界きっての数学ヲタク！アルキメデス～
古代の数学者を語る上で欠かせないのが、古代ギリシャの数学者アルキメデスです。

アルキメデス

彼は紀元前２５０年頃に活躍した数学者で、「アルキメデスの浮力の原理」が一番有名だと思います。

～ ヘウレーカ！アルキメデスの浮力の原理 ～
　ある日アルキメデスは王様からこのような依頼を受けました。
「金細工職人に金の王冠を作らせたのだが、私はこの王冠に銀が混ざっているのではないかと思っている。この王冠が純金で出来ているのか、銀との混ざりものなのかを調べよ。」
　アルキメデスは「同体積において、金は銀より重い」ことは知っていたが、それを調べるためには、王冠を一度溶かして立方体にし、体積を調べる必要があった。そのようなことが出来ないことは明白であったため、アルキメデスは悩んだ。
　ある日、悩みつかれたアルキメデスは風呂に入り疲れを癒していたところ、「風呂に入ると、自分の体積の分だけ水面が上がり、縁から流れ出る」ことに気がついた。「王冠を水に入れ、あふれた分の体積を調べれば・・・。ヘウレーカ！（わかったぞ！）」と全裸のまま王様に報告をしに行ったのであった。
　こうしてアルキメデスは、金細工職人が作った王冠が銀の混ざりものであることを証明し、王様の依頼を達成したのであった。

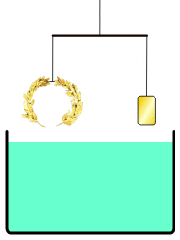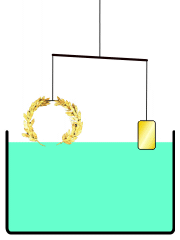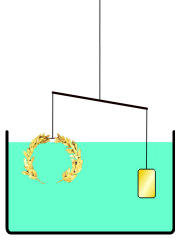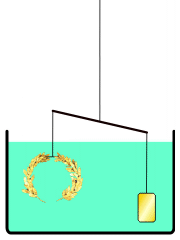
同じ体積の王冠と金を水に沈めると、銀が混ざった王冠の方が質量が小さいので、浮いてしまう。

　この浮力の原理の発見により、「舟が水に浮かぶ理由」が分かった古代ギリシャ人は、浮力の原理を応用し、戦艦を作ることに成功する。彼らの国は海上戦において無類の力を発揮した。

～発明王アルキメデス～
　他にもアルキメデスは、幾何学的な考えと物理への応用によって様々な発明をしている。例えば近現代の水流管理で活躍した「アルキメディアンスクリュー」が挙げられる。

従来、下にあるものを上に移動させるとき「持ち上げる必要がある」ことから、シーソーのようにてこの原理で持ち上げることが多かった中、、アルキメデスは「回転の力」を使うことによって上昇機構を作れるのではと考案した。

　アルキメデスが最初に考えたのは「滑車」である。車輪にロープをかけ、力を加える方向を一方向にすることによって、力の加え方の効率化を示した。
　さらに「回転の力」を効率よく伝える方法はないかと考案したのが「アルキメディアンスクリュー」である。

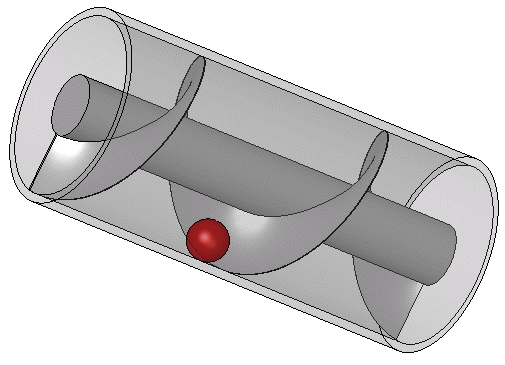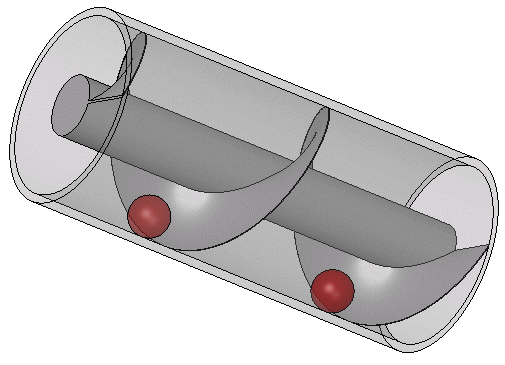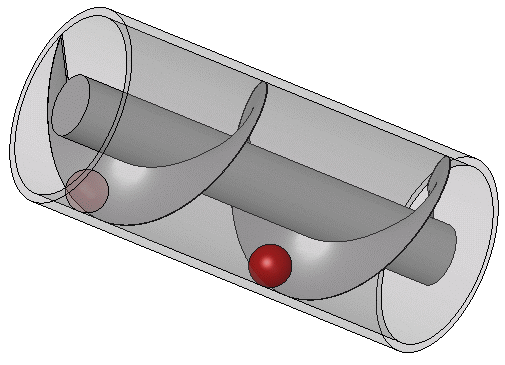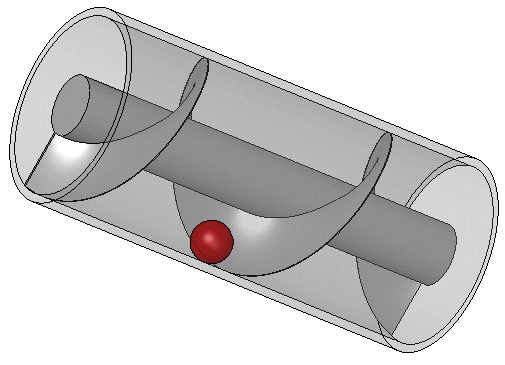
アルキメディアンスクリューの仕組み

　このアルキメディアンスクリューの画期的な点は、滑車だと物を持ち上げるときに上下運動が必要であることに対して、同じ方向に回転をし続けるだけで効力を発揮する点にある。このスクリュー機構は現代でも水を汲み上げる際に使われたり、応用系として水力発電に使われたりしている。「古代だからバケツで水を汲み上げることしか出来なかった」なんていうことは全く無く、現代でも利用されるほど発展していたのである。

～古代のロマン砲！アルキメデスの熱光線～
　白兵戦ではなく海上戦となったとき、遠距離から敵艦を沈められたら・・・。そのようなことを思ったことはありませんか？（いや、無い）そんなときに活躍するのがアルキメデスの熱光線です！浮力の原理の発見や滑車・アルキメディアンスクリューの開発を行ったアルキメデスは政治上・戦略上最重要人物として、この時代に存在していました。当時他国と戦争を行っていた自国は対軍艦兵器の開発をアルキメデスに依頼しました。するとアルキメデスは「太陽の光を多数の鏡とレンズを用いて反射し、敵艦に焦点を合わせ炎上させる」という方法を用いました。これがアルキメデスの熱光線と呼ばれるものです。

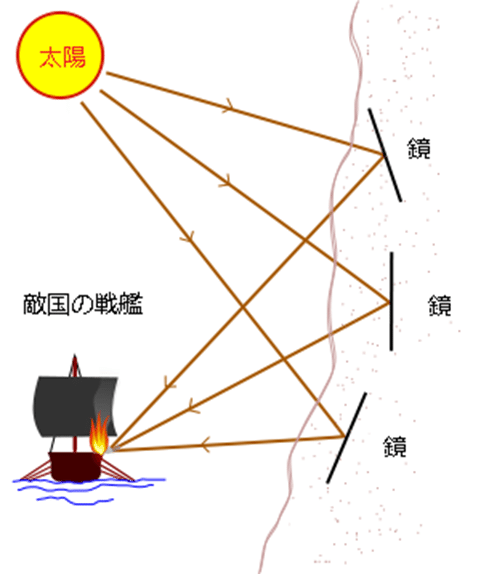
アルキメデスの熱光線のイメージ図

　こんな方法で敵艦を炎上できるはずが無いという否定的な意見も多いですが、

こちらの動画を見てみると・・・。燃えている。木のみならず金属すら貫通している・・・。屈折・反射・焦点の考えがあればあるいは本当にアルキメデスはこのロマン砲を用いて敵を撃退したのかもしれませんね。

　晩年は円周率に興味を持ち、円周率がだいたいどれくらいの数になるかと円に対する内接正多角形と外接正多角形を用いて3 10/71<π<3 1/7であることを示した。(小数で表すと 3.14084 < π < 3.14286となる。)

そんなアルキメデスの最期は、自国が敗戦国になってしまった中、地面に円を描き思考を巡らせていたところ、「貴様がアルキメデスかっ！！」と敵国の兵士が勢い余ってアルキメデスの円を踏んでしまったところ、「私の円を乱すなっ！！」と罵倒し兵士に切り殺されてしまいました。その敵国の兵士も最重要人物であるアルキメデスを捕らえるよう命令を受け、意気揚々としていたこともあり、アルキメデスにとっても兵士にとっても可哀そうな結末となってしまった。

～地球の形は平面？球体？エラトステネス！～
　皆さんは「エラトステネスのふるい」をご存じだろうか？

エラトステネスのふるいの仕方

　この「エラトステネスのふるい」で有名なのが、紀元前２５０年頃からエジプトで活躍した古代ギリシャ人のエラトステネスです。数学的に性質の強い素数に注目をし、その判定法を考案しただけでもすごいのですが、彼が古代の数学者を語る上で外せない理由は「世界で初めて地球の大きさを計算した」ことにあります。

エラトステネス

　彼は当時「地球は平面であり、天がこの大地を中心に回っている（天動説）」と考えるのが当たり前な中「もしかすると地球は球体なのかもしれない」と仮説を立てました。そこで彼はアキクサンドリアとシエナという二つの都市で「同じ時間の影の伸び方を比較する」という方法を用いました。

　実際はシエナで影ができない時刻にアレキサンドリアでは影が出来ていたことから、地球が球体であると考え、アレキサンドリアとシエナの距離と影の長さ、棒や深い井戸を用いて角度を計測したうえで地球の円周を考えると

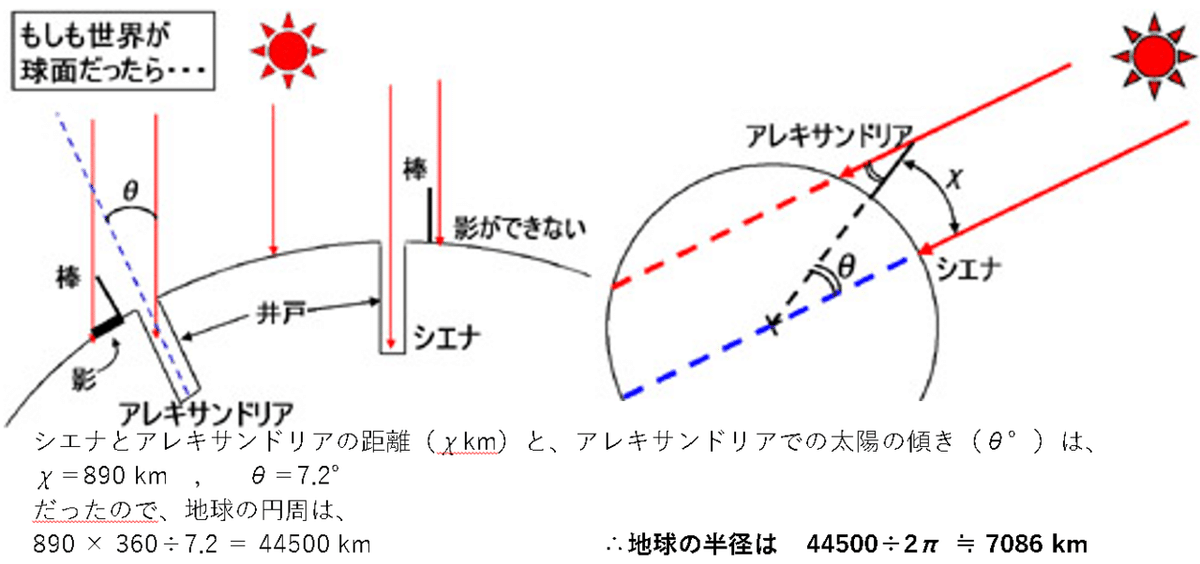
　このようになりました。実際は約40,075 kmなので、誤差はありますがエラトステネスは２３００年も昔に地球が球体であることと、どれくらいの大きさなのかを計算で出してしまったのです！
　この頃から地動説がとなえられるようになったのですが、この話を聞いている人には「あれ？でも地動説ってガリレオが考えたんじゃ・・・。」と思う人もいるでしょう。地動説が普及しなかった原因としては天動説派が多かったことと宗教上の理由があったと言われています。

　今回は、古代の数学者を語る上で欠かせない二人アルキメデスとエラトステネスについてお話ししました。彼らが去った後、宗教の普及に反比例し数学は発展がほぼ無い暗黒時代に直面します。
次回は約１０００年後であるA.D.８００年頃、暗黒時代を打破と共に新しい数学のお話をします！数学が好きな人も、数学に少しでも興味が沸いた人も、また見てくださいね！