
そういえばあれ何だっけという「すうがく」の判別式D=b^2-4acを見た目で理解できるように端的に書いてみた
起立、気をつけ、礼
はい!前回のノート見てみて~
と進みますよねっ授業って笑
はぁ~い(ぼる塾の田辺さん風)では改めて
今日の準備はこれ!
^ は? 例えば5^2 = 5 × 5 のように計算する二乗のことだ
ということで、b^2=b×bですよ、理解してくださいね~
(パソコンだとこんな表し方をします)
少し数学に触れた気がしませんか?笑笑
最後まで読んでくださいね~
さて、中学校時代に習った知識で、本日は高校数学(数学Ⅰ)に登場する
「判別式D=b^2-4ac」
をできる限り見た目「👀」で分かるように解説でなく、理解する、で進めていこうと思います!
やってもいいかなぁ~ いいとも!(古っ💦
まず2次方程式 ax^2+bx+c=0 について解くとx=
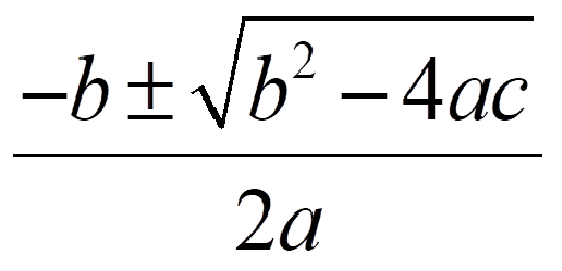
中学校で2次方程式を勉強したときに、
「解の公式」っ言われますよね
さて、ここからが今日の本番!
解の個数の違い、判りますか? 多分、この言い方が意味不明なんですよね、そこで、下の3つの解の違いはどこの部分でしょうか?
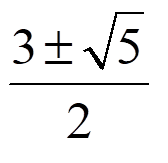
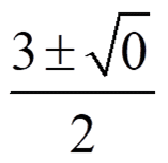
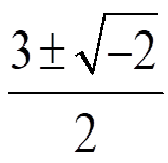
どうでしょうか? わかった人??
そう!
ルートの中~、「ルートの中~」って言ってくれましたか?👍
改めて並べてみると良く判りますよね!
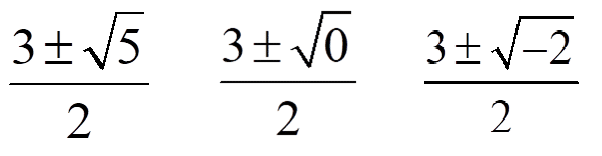
解の個数が2次方程式には
2個、1個、解なしの場合が存在するということですかね~ やった~やった~ヤッターマン♪
ルートの中の値が、ーの値(負)であるとき、ルートの値は存在しないので解はなしとします <数学Ⅰにおいて>
ここまでの流れを か く に ん !
ルートの中の数字によって、2次方程式の解の個数が変わるんだ!
ルートの中の数字が「0」であれば1個 を中心に考えると
ルートの中の数字が「+」か「-」で解の個数は「2個」か「0個」となる
0という数字が境目👀ですね!
解の個数を判別する式 discriminant の頭文字を取り、判別式と言います、そしてD で表します その式が、b^2-4ac です
解の公式の、ルートの中の式「b^2-4ac」 を、Dで表し「判別式」というわけです!(*・ω・)(*-ω-)(*・ω・)(*-ω-)ウンウン♪
※2次関数において、X軸との関係で、判別式が登場しちゃいます✨
つまり、2次関数とX軸の交点の個数が「2個、1個、0個」!
もしかしたらここまで読んでいただけたら、あって気付いた方がいるかもしれませんが、
実は、2次方程式 ax^2+bx+c=0の
左辺と右辺に注目してみると
y=ax^2+bx+c という2次関数、
y= 0 という X軸 のことを表してます
そう、この「2つの関数の関係」が、2次方程式の本来の意味。つまり、2次方程式を解けという、問の解(例えばx=3)は、2次関数とX軸との交点のX座標を求めていた!ということになりますね♬
<例えば、交点(3,★)ということ ★:この場合は適当な数>
1次方程式は、1次関数と X軸 の交点のX座標を求めていたということになります!
n次方程式においても、 n次関数とX軸との交点のX座標を求めていたということです
ということで、
判別式は、皆さんが必ず1回は覚えたであろう、解の公式のルートの中の式のことを表すんだ!ということを判ってくださいね~

◎解の公式や判別式を語呂合わせすることで覚えた記憶がないのですが、もしあるとすれば、「判別式D=美人の良い足」と言っている先生もいます笑
語呂合わせなど受験で必要な技術ですからね❣ 是非色々な語呂合わせを探してみましょう!じゃんじゃん笑
たまにの「数学」っていかがでしたか? 個人的には、+とーを区別をする「0」という数字は凄いと思います!またお会いしましょう~
GoodNight✨

